线性方程求解方法
Gauss消去法

1转化为(同解)的三角形方程组
2化阶梯形矩阵 且 要保证解不变,所以需要组成增广阵再进行 初等行变换(同解变换)
实际过程就是一行一行消元,用上面行消去下面行第一个项,有利于解出最后一个回代
举例:
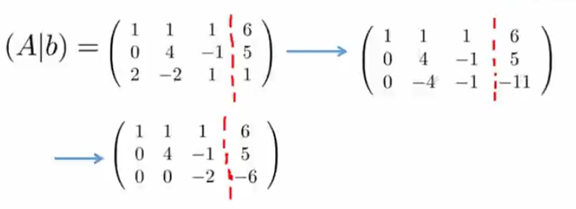
适用性:
系数矩阵A规模比较小的,否则很慢
系数矩阵A是非奇异的,否则没有唯一解
Jacobi迭代法


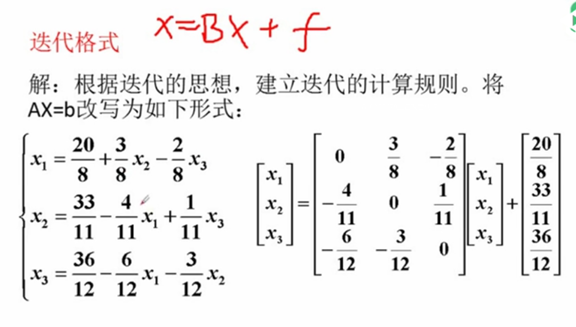


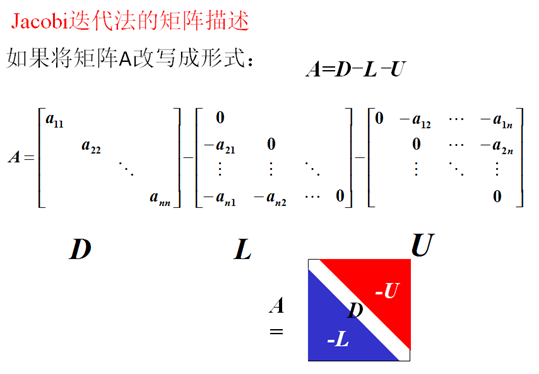
雅克比迭代法矩阵描述
矩阵迭代公式

DX = (L+U)X + b
L和U都没更新,写在右边
Gauss-Seildel迭代法

及时更新下半三角系数的迭代
矩阵迭代公式一

(D-L)X = UX + b
只有上半部的U没更新,写在右边
矩阵迭代公式二

这样D的逆更方便求出来
迭代法的收敛
严格对角占优矩阵
定义:对角线元素的绝对值和 > 其所在 行/列 元素的绝对值和 的矩阵
