一、直线
直线方程
| 方程名称 | 形式 | 说明 |
|---|---|---|
| 一般式 | ax+by+c=0 | 优点:可以表示平面上的任意一条直线缺点:要确定的常数较多 |
| 斜截式 | y=kx+b | 优点:只需要斜率和截距缺点:不能表示垂直x轴的直线x=a |
| 点斜式 | y-y0=k(x-x0) | 优点:只需要一个点和斜率缺点:不能表示垂直x轴的直线x=a |
| 两点式 | (y-y1)/(y2-y1)=(x-x1)/(x2-x1) | 优点:只需要2个点缺点:不能表示两点x1=x2或y1=y2时的直线(即垂直或水平直线) |
| 截距式 | x/a+y/b=1 | 优点:只需要x轴截距a和y轴截距b缺点:不能表示截距为0时的直线,比如正比例直线 |
二、平面
平面方程常用4种
| 方程名称 | 形式 | 说明 |
|---|---|---|
| 一般式 | Ax+By+Cz+D=0 | |
| 截距式 | x/a+y/b+z/c=1 | |
| 点法式 | A(x-x0)+B(y-y0)+C(z-z0)=0 | 向量(A,B,C)为平面的法向量 |
| 法线式 | xcosα+ycosβ+zcosγ=p | 其中cosα、cosβ、cosγ是平面法矢量的方向余弦,p为原点到平面的距离。 |
平面方程全部7种
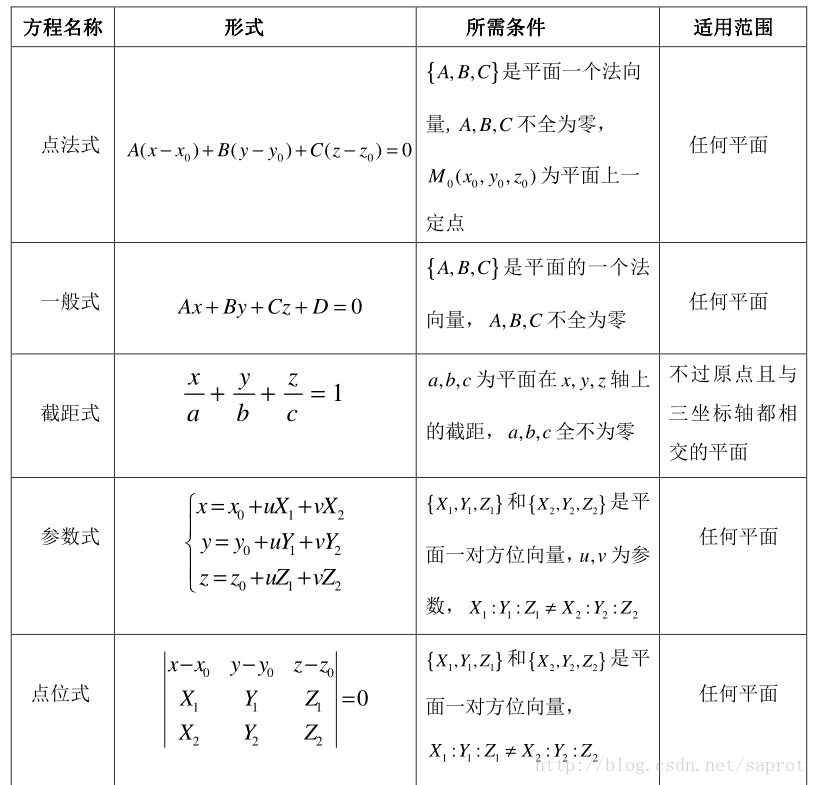

三、超平面
二维空间的超平面是一条直线,三维空间的超平面是一个平面,而N维空间的超平面则是N-1维的仿射空间。