向量
向量内积 和 投影
内积:
1用点乘:a•b
2用转置乘:a^T b
3向量的模是范数的一种
4 wT w《=》向量自己做内积 = 自身长度(模)²,因为投影结果还是w向量本身
投影:
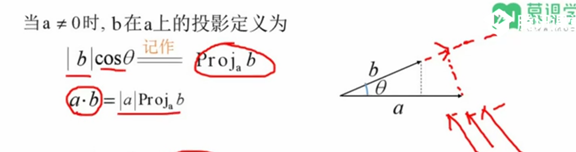
1 b在a上的投影 = |b|cosθ
2 内积 = 向量1在向量2上的投影 * 他的长度(模,绝对值符号);
3 由2又有:b在a上的投影 = $\frac {a^T b} {||a||}$ ★
向量外积
向量范数
- 向量范数的定义和性质:

齐次性:数乘以后会放大相应的倍数
- 1-范数、2-范数、无穷范数:
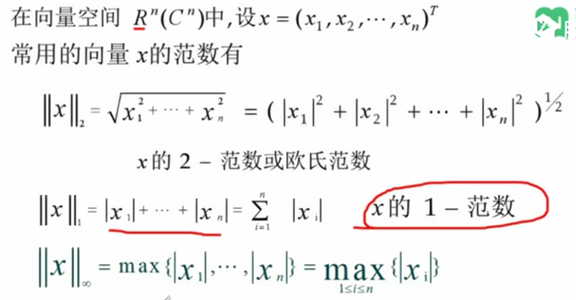
- 稀疏性 和 0-范数:

稀疏性用到的范数:
特殊的0-范数,他不满足齐次性;
所以需要1-范数来辅助解决;
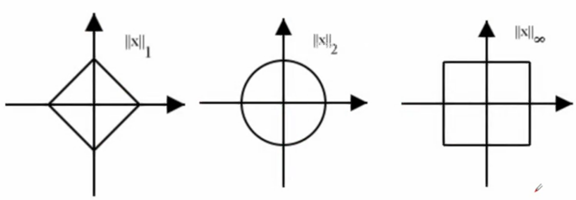
- 范数的几何意义:

向量组
- 初始单位向两组

- 向量组等价

- 线性相关 和 线性无关

- 施密特正交化

由施密特正交化生成的 正交向量组 和 之前的线性无关向量组 可以互相线性表示
