发表于 | Edited on | 分类于 | 评论数：

数据挖掘——信用卡欺诈检测

案例：用 逻辑回归 预测 信用卡欺诈

1
2
3
4
5
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

%matplotlib inline
1
2
data = pd.read_csv("creditcard.csv")
data.head()
Time V1 V2 V3 V4 V5 V6 V7 V8 V9 ... V21 V22 V23 V24 V25 V26 V27 V28 Amount Class
0 0.0 -1.359807 -0.072781 2.536347 1.378155 -0.338321 0.462388 0.239599 0.098698 0.363787 ... -0.018307 0.277838 -0.110474 0.066928 0.128539 -0.189115 0.133558 -0.021053 149.62 0
1 0.0 1.191857 0.266151 0.166480 0.448154 0.060018 -0.082361 -0.078803 0.085102 -0.255425 ... -0.225775 -0.638672 0.101288 -0.339846 0.167170 0.125895 -0.008983 0.014724 2.69 0
2 1.0 -1.358354 -1.340163 1.773209 0.379780 -0.503198 1.800499 0.791461 0.247676 -1.514654 ... 0.247998 0.771679 0.909412 -0.689281 -0.327642 -0.139097 -0.055353 -0.059752 378.66 0
3 1.0 -0.966272 -0.185226 1.792993 -0.863291 -0.010309 1.247203 0.237609 0.377436 -1.387024 ... -0.108300 0.005274 -0.190321 -1.175575 0.647376 -0.221929 0.062723 0.061458 123.50 0
4 2.0 -1.158233 0.877737 1.548718 0.403034 -0.407193 0.095921 0.592941 -0.270533 0.817739 ... -0.009431 0.798278 -0.137458 0.141267 -0.206010 0.502292 0.219422 0.215153 69.99 0

5 rows × 31 columns

1数据预处理——归一化、去掉不用的列

1
2
3
4
5
6
7
8
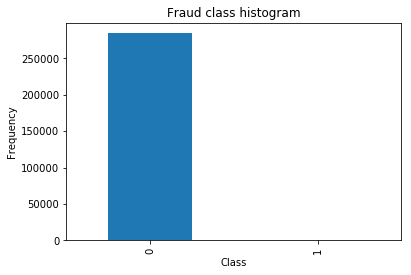
9
count_classes = pd.value_counts(data['Class'], sort = True).sort_index()
count_classes.plot(kind = 'bar')
plt.title("Fraud class histogram")
plt.xlabel("Class")
plt.ylabel("Frequency")
#发现样本分布十分不均衡
#策略：统一不同类别样本总数 
#1）oversample——过采样，把少的增多 
#2) undersample——欠采样，把多的减少
<matplotlib.text.Text at 0x5d32f27ef0>

png

1
2
3
4
5
6
#用sklearn 函数来进行归一化(自带合并到原dataframe功能)
from sklearn.preprocessing import StandardScaler  

data['normAmount'] = StandardScaler().fit_transform(data['Amount'].values.reshape(-1, 1))
data = data.drop(['Time','Amount'],axis=1)
data.head()
V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 ... V21 V22 V23 V24 V25 V26 V27 V28 Class normAmount
0 -1.359807 -0.072781 2.536347 1.378155 -0.338321 0.462388 0.239599 0.098698 0.363787 0.090794 ... -0.018307 0.277838 -0.110474 0.066928 0.128539 -0.189115 0.133558 -0.021053 0 0.244964
1 1.191857 0.266151 0.166480 0.448154 0.060018 -0.082361 -0.078803 0.085102 -0.255425 -0.166974 ... -0.225775 -0.638672 0.101288 -0.339846 0.167170 0.125895 -0.008983 0.014724 0 -0.342475
2 -1.358354 -1.340163 1.773209 0.379780 -0.503198 1.800499 0.791461 0.247676 -1.514654 0.207643 ... 0.247998 0.771679 0.909412 -0.689281 -0.327642 -0.139097 -0.055353 -0.059752 0 1.160686
3 -0.966272 -0.185226 1.792993 -0.863291 -0.010309 1.247203 0.237609 0.377436 -1.387024 -0.054952 ... -0.108300 0.005274 -0.190321 -1.175575 0.647376 -0.221929 0.062723 0.061458 0 0.140534
4 -1.158233 0.877737 1.548718 0.403034 -0.407193 0.095921 0.592941 -0.270533 0.817739 0.753074 ... -0.009431 0.798278 -0.137458 0.141267 -0.206010 0.502292 0.219422 0.215153 0 -0.073403

5 rows × 30 columns

1数据预处理——解决样本分布不均衡问题之undersample

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 方式一：采用“undersample”构建模型

#把数据集切分为 样本 和 标记 存变量
X = data.loc[:, data.columns != 'Class']
y = data.loc[:, data.columns == 'Class']

#计算欺诈样本总数
number_records_fraud = len(data[data.Class == 1])  
#取得欺诈行为的样本index
fraud_indices = np.array(data[data.Class == 1].index)  

#取得正常的样本index
normal_indices = data[data.Class == 0].index   

# 随机选出 和 欺诈类数量相同的 正常Index
random_normal_indices = np.random.choice(normal_indices, number_records_fraud, replace = False)
random_normal_indices = np.array(random_normal_indices)

# 合并取得的两组index，作为欠采样index
under_sample_indices = np.concatenate([fraud_indices,random_normal_indices])

# 取得欠采样dataset
under_sample_data = data.iloc[under_sample_indices,:]

#把undersample数据集切分为 样本 和 标记 存变量
X_undersample = under_sample_data.loc[:, under_sample_data.columns != 'Class']
y_undersample = under_sample_data.loc[:, under_sample_data.columns == 'Class']

# 显示处理结果
print("Percentage of normal transactions: ", len(under_sample_data[under_sample_data.Class == 0])/len(under_sample_data))
print("Percentage of fraud transactions: ", len(under_sample_data[under_sample_data.Class == 1])/len(under_sample_data))
print("Total number of transactions in resampled data: ", len(under_sample_data))
Percentage of normal transactions:  0.5
Percentage of fraud transactions:  0.5
Total number of transactions in resampled data:  984

1数据预处理——划分训练和测试集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#引入数据集切分函数
from sklearn.cross_validation import train_test_split

# Whole dataset 划分全部数据
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3, random_state = 0)

print("Number transactions train dataset: ", len(X_train))
print("Number transactions test dataset: ", len(X_test))
print("Total number of transactions: ", len(X_train)+len(X_test))

# Undersampled dataset 划分欠采样数据
X_train_undersample, X_test_undersample, y_train_undersample, y_test_undersample = train_test_split(X_undersample
                                                                                                   ,y_undersample
                                                                                                   ,test_size = 0.3
                                                                                                   ,random_state = 0)

print("")
print("Number transactions train dataset: ", len(X_train_undersample))
print("Number transactions test dataset: ", len(X_test_undersample))
print("Total number of transactions: ", len(X_train_undersample)+len(X_test_undersample))
Number transactions train dataset:  199364
Number transactions test dataset:  85443
Total number of transactions:  284807

Number transactions train dataset:  688
Number transactions test dataset:  296
Total number of transactions:  984

2 交叉验证——在训练集上做，找最好的逻辑回归正则惩罚系数C

1
2
3
4
#Recall = TP/(TP+FN)  这里适用召回率来检测
from sklearn.linear_model import LogisticRegression
from sklearn.cross_validation import KFold, cross_val_score
from sklearn.metrics import confusion_matrix,recall_score,classification_report
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
# 自己实现召回率的 K=5的交叉验证函数（注意：此处是在训练集上的交叉验证）
def printing_Kfold_scores(x_train_data,y_train_data):
    fold = KFold(len(y_train_data),5,shuffle=False) 

    # Different C parameters   
    #在sklearn里面，惩罚系数是倒数，比如100其实是0.01
    #每个都试一遍，看哪个模型最好
    c_param_range = [0.01,0.1,1,10,100]

    results_table = pd.DataFrame(index = range(len(c_param_range),2), columns = ['C_parameter','Mean recall score'])
    results_table['C_parameter'] = c_param_range

    # the k-fold will give 2 lists: train_indices = indices[0], test_indices = indices[1]
    j = 0
    for c_param in c_param_range:
        print('-------------------------------------------')
        print('C parameter: ', c_param)
        print('-------------------------------------------')
        print('')

        recall_accs = []
        # iteration：迭代轮数1-5
        # indices：[0]表示训练集索引集合，[1]表示测试集索引集合
        for iteration, indices in enumerate(fold,start=1):

            # Call the logistic regression model with a certain C parameter
            # C：指定惩罚项的参数
            # penalty：指定惩罚项的算法
            lr = LogisticRegression(C = c_param, penalty = 'l1')

            # Use the training data to fit the model. In this case, we use the portion of the fold to train the model
            # with indices[0]. We then predict on the portion assigned as the 'test cross validation' with indices[1]
            lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())

            # Predict values using the test indices in the training data
            y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values)

            # Calculate the recall score and append it to a list for recall scores representing the current c_parameter
            recall_acc = recall_score(y_train_data.iloc[indices[1],:].values,y_pred_undersample)
            recall_accs.append(recall_acc)
            print('Iteration ', iteration,': recall score = ', recall_acc)

        # The mean value of those recall scores is the metric we want to save and get hold of.
        results_table.loc[j,'Mean recall score'] = np.mean(recall_accs)
        j += 1
        print('')
        print('Mean recall score ', np.mean(recall_accs))
        print('')

    best_c = results_table.loc[results_table['Mean recall score'].idxmax()]['C_parameter']
    
    # Finally, we can check which C parameter is the best amongst the chosen.
    print('*********************************************************************************')
    print('Best model to choose from cross validation is with C parameter = ', best_c)
    print('*********************************************************************************')
    
    return best_c
1
best_c = printing_Kfold_scores(X_train_undersample,y_train_undersample)
-------------------------------------------
C parameter:  0.01
-------------------------------------------

Iteration  1 : recall score =  0.931506849315
Iteration  2 : recall score =  0.931506849315
Iteration  3 : recall score =  1.0
Iteration  4 : recall score =  0.972972972973
Iteration  5 : recall score =  0.969696969697

Mean recall score  0.96113672826

-------------------------------------------
C parameter:  0.1
-------------------------------------------

Iteration  1 : recall score =  0.849315068493
Iteration  2 : recall score =  0.86301369863
Iteration  3 : recall score =  0.932203389831
Iteration  4 : recall score =  0.945945945946
Iteration  5 : recall score =  0.893939393939

Mean recall score  0.896883499368

-------------------------------------------
C parameter:  1
-------------------------------------------

Iteration  1 : recall score =  0.86301369863
Iteration  2 : recall score =  0.890410958904
Iteration  3 : recall score =  0.983050847458
Iteration  4 : recall score =  0.945945945946
Iteration  5 : recall score =  0.909090909091

Mean recall score  0.918302472006

-------------------------------------------
C parameter:  10
-------------------------------------------

Iteration  1 : recall score =  0.86301369863
Iteration  2 : recall score =  0.904109589041
Iteration  3 : recall score =  0.983050847458
Iteration  4 : recall score =  0.945945945946
Iteration  5 : recall score =  0.909090909091

Mean recall score  0.921042198033

-------------------------------------------
C parameter:  100
-------------------------------------------

Iteration  1 : recall score =  0.876712328767
Iteration  2 : recall score =  0.890410958904
Iteration  3 : recall score =  0.983050847458
Iteration  4 : recall score =  0.945945945946
Iteration  5 : recall score =  0.909090909091

Mean recall score  0.921042198033

*********************************************************************************
Best model to choose from cross validation is with C parameter =  0.01
*********************************************************************************

3训练 + 测试——用best_C在训练集上重新训练一遍，再在undersample测试集上预测用 混淆矩阵 计算recall值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import itertools
def plot_confusion_matrix(cm, classes,
                          title='Confusion matrix',
                          cmap=plt.cm.Blues):
    """
    This function prints and plots the confusion matrix.
    """
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=0)
    plt.yticks(tick_marks, classes)

    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, cm[i, j],
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_undersample = lr.predict(X_test_undersample.values)

# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test_undersample,y_pred_undersample)
np.set_printoptions(precision=2)

print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
                      , classes=class_names
                      , title='Confusion matrix')
plt.show()
#混淆矩阵 显示模型分类效果
Recall metric in the testing dataset:  0.931972789116

png

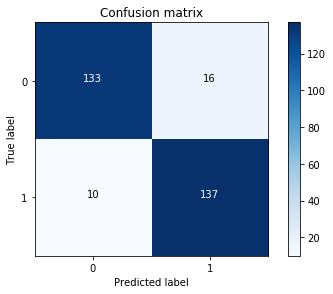
3训练 + 测试——用best_C在训练集上重新训练一遍，再在 完整 测试集上预测用 混淆矩阵 计算recall值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred = lr.predict(X_test.values)

# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test,y_pred)
np.set_printoptions(precision=2)

print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
                      , classes=class_names
                      , title='Confusion matrix')
plt.show()
Recall metric in the testing dataset:  0.918367346939

png

1
2
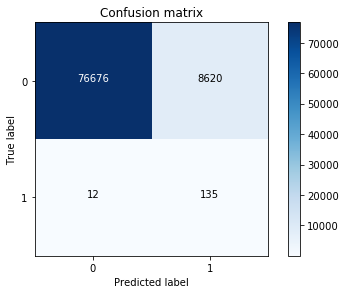
这里发现虽然recall值还可以，但是误伤了8581个（被检测成欺诈了），也就是精度accuracy有点低。
故要权衡两者，都要较高才行

这里展示的是：不做样本平衡处理，直接把所有样本做交叉验证，发现效果很差

1
best_c = printing_Kfold_scores(X_train,y_train)
-------------------------------------------
C parameter:  0.01
-------------------------------------------

Iteration  1 : recall score =  0.492537313433
Iteration  2 : recall score =  0.602739726027
Iteration  3 : recall score =  0.683333333333
Iteration  4 : recall score =  0.569230769231
Iteration  5 : recall score =  0.45

Mean recall score  0.559568228405

-------------------------------------------
C parameter:  0.1
-------------------------------------------

Iteration  1 : recall score =  0.567164179104
Iteration  2 : recall score =  0.616438356164
Iteration  3 : recall score =  0.683333333333
Iteration  4 : recall score =  0.584615384615
Iteration  5 : recall score =  0.525

Mean recall score  0.595310250644

-------------------------------------------
C parameter:  1
-------------------------------------------

Iteration  1 : recall score =  0.55223880597
Iteration  2 : recall score =  0.616438356164
Iteration  3 : recall score =  0.716666666667
Iteration  4 : recall score =  0.615384615385
Iteration  5 : recall score =  0.5625

Mean recall score  0.612645688837

-------------------------------------------
C parameter:  10
-------------------------------------------

Iteration  1 : recall score =  0.55223880597
Iteration  2 : recall score =  0.616438356164
Iteration  3 : recall score =  0.733333333333
Iteration  4 : recall score =  0.615384615385
Iteration  5 : recall score =  0.575

Mean recall score  0.61847902217

-------------------------------------------
C parameter:  100
-------------------------------------------

Iteration  1 : recall score =  0.55223880597
Iteration  2 : recall score =  0.616438356164
Iteration  3 : recall score =  0.733333333333
Iteration  4 : recall score =  0.615384615385
Iteration  5 : recall score =  0.575

Mean recall score  0.61847902217

*********************************************************************************
Best model to choose from cross validation is with C parameter =  10.0
*********************************************************************************

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(X_train,y_train.values.ravel())
y_pred_undersample = lr.predict(X_test.values)

# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test,y_pred_undersample)
np.set_printoptions(precision=2)

print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
                      , classes=class_names
                      , title='Confusion matrix')
plt.show()
Recall metric in the testing dataset:  0.619047619048

png

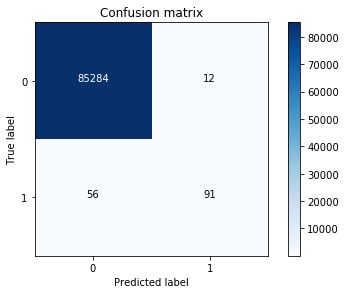
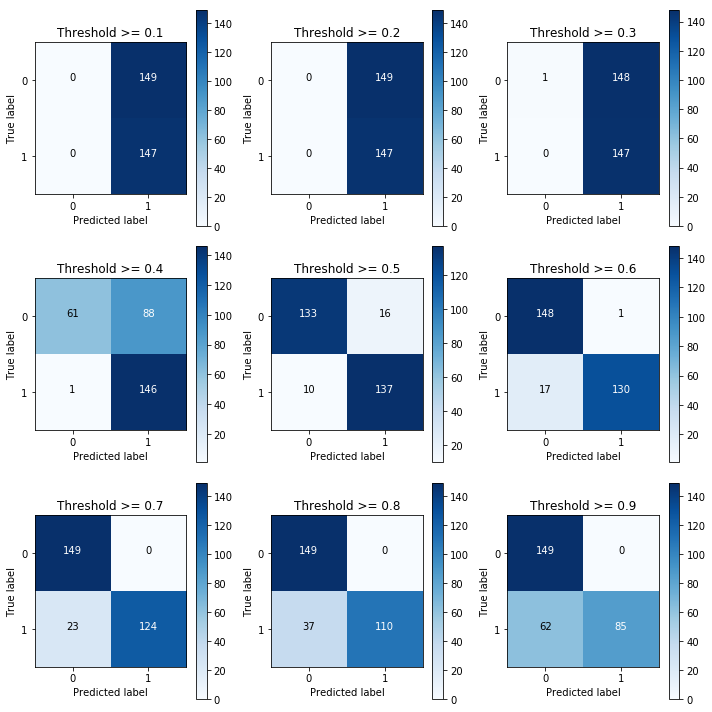
4 用predict_proba来测试 最好的逻辑回归 阈值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
lr = LogisticRegression(C = 0.01, penalty = 'l1')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_undersample_proba = lr.predict_proba(X_test_undersample.values)

thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]

plt.figure(figsize=(10,10))

j = 1
for threshold in thresholds:
    y_test_predictions_high_recall = y_pred_undersample_proba[:,1] > threshold
    
    plt.subplot(3,3,j)
    j += 1
    
    # Compute confusion matrix
    cnf_matrix = confusion_matrix(y_test_undersample,y_test_predictions_high_recall)
    np.set_printoptions(precision=2)

    print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

    # Plot non-normalized confusion matrix
    class_names = [0,1]
    plot_confusion_matrix(cnf_matrix
                          , classes=class_names
                          , title='Threshold >= %s'%threshold)
Recall metric in the testing dataset:  1.0
Recall metric in the testing dataset:  1.0
Recall metric in the testing dataset:  1.0
Recall metric in the testing dataset:  0.993197278912
Recall metric in the testing dataset:  0.931972789116
Recall metric in the testing dataset:  0.884353741497
Recall metric in the testing dataset:  0.843537414966
Recall metric in the testing dataset:  0.748299319728
Recall metric in the testing dataset:  0.578231292517

png

1数据预处理——解决样本分布不均衡问题之oversample

1
2
3
4
5
6
import pandas as pd
# 安装命令：pip install imblearn
from imblearn.over_sampling import SMOTE
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
1
2
3
4
5
6
7
8
credit_cards=pd.read_csv('creditcard.csv')

columns=credit_cards.columns
# The labels are in the last column ('Class'). Simply remove it to obtain features columns
features_columns=columns.delete(len(columns)-1)

features=credit_cards[features_columns]
labels=credit_cards['Class']
1
2
3
4
5
#划分数据集
features_train, features_test, labels_train, labels_test = train_test_split(features, 
                                                                            labels, 
                                                                            test_size=0.2, 
                                                                            random_state=0)
1
2
3
#★SMOTE算法通过给定的训练集，生成新的随机扩充训练集
oversampler=SMOTE(random_state=0)
os_features,os_labels=oversampler.fit_sample(features_train,labels_train)
1
2
3
4
5
#生成前，label=0
print(len(labels_train[labels_train == 0]))

#生成以后，label=1的变成和=0的一样多
print(len(os_labels[os_labels == 1]))
227454
227454

1
2
3
os_features = pd.DataFrame(os_features)
os_labels = pd.DataFrame(os_labels)
best_c = printing_Kfold_scores(os_features,os_labels)
-------------------------------------------
C parameter:  0.01
-------------------------------------------

Iteration  1 : recall score =  0.890322580645
Iteration  2 : recall score =  0.894736842105
Iteration  3 : recall score =  0.968617904172
Iteration  4 : recall score =  0.944471922709
Iteration  5 : recall score =  0.958397907255

Mean recall score  0.931309431377

-------------------------------------------
C parameter:  0.1
-------------------------------------------

Iteration  1 : recall score =  0.890322580645
Iteration  2 : recall score =  0.894736842105
Iteration  3 : recall score =  0.970255615802
Iteration  4 : recall score =  0.959991646608
Iteration  5 : recall score =  0.96051922929

Mean recall score  0.93516518289

-------------------------------------------
C parameter:  1
-------------------------------------------

Iteration  1 : recall score =  0.890322580645
Iteration  2 : recall score =  0.894736842105
Iteration  3 : recall score =  0.970211353325
Iteration  4 : recall score =  0.960134533584
Iteration  5 : recall score =  0.960442290148

Mean recall score  0.935169519962

-------------------------------------------
C parameter:  10
-------------------------------------------

Iteration  1 : recall score =  0.890322580645
Iteration  2 : recall score =  0.894736842105
Iteration  3 : recall score =  0.970322009516
Iteration  4 : recall score =  0.95977182049
Iteration  5 : recall score =  0.960783020631

Mean recall score  0.935187254678

-------------------------------------------
C parameter:  100
-------------------------------------------

Iteration  1 : recall score =  0.890322580645
Iteration  2 : recall score =  0.894736842105
Iteration  3 : recall score =  0.969635941131
Iteration  4 : recall score =  0.960255437949
Iteration  5 : recall score =  0.960398324925

Mean recall score  0.935069825351

*********************************************************************************
Best model to choose from cross validation is with C parameter =  10.0
*********************************************************************************

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(os_features,os_labels.values.ravel())
y_pred = lr.predict(features_test.values)

# Compute confusion matrix
cnf_matrix = confusion_matrix(labels_test,y_pred)
np.set_printoptions(precision=2)

print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
                      , classes=class_names
                      , title='Confusion matrix')
plt.show()
Recall metric in the testing dataset:  0.910891089109

png

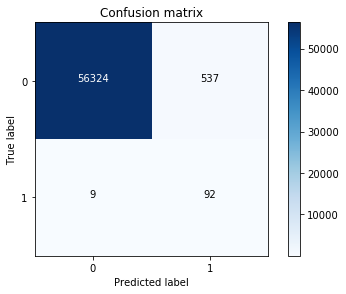
1
2


1
2


1
2


꧁༺The༒End༻꧂